El efecto Coriolis, descrito en 1835 por el científico francés Gaspard-Gustave Coriolis, es el efecto que se observa en un sistema de referencia en rotación (y por tanto no inercial) cuando un cuerpo se encuentra en movimiento respecto de dicho sistema de referencia. Este efecto consiste en la existencia de una aceleración relativa del cuerpo en dicho el sistema en rotación. Esta aceleración es siempre perpendicular al eje de rotación del sistema y a la velocidad del cuerpo.
El efecto Coriolis hace que un objeto que se mueve sobre el radio de un disco en rotación tienda a acelerarse con respecto a ese disco según si el movimiento es hacia el eje de giro o alejándose de éste. Por el mismo principio, en el caso de una esfera en rotación, el movimiento de un objeto sobre los meridianos también presenta este efecto, ya que dicho movimiento reduce o incrementa la distancia respecto al eje de giro de la esfera.
Debido a que el objeto sufre una aceleración desde el punto de vista del observador en rotación, es como si para éste existiera una fuerza sobre el objeto que lo acelera. A esta fuerza se la llama fuerza de Coriolis, y no es una fuerza real en el sentido de que no hay nada que la produzca. Se trata pues de una fuerza inercial o ficticia, que se introduce para explicar, desde el punto de vista del sistema en rotación, la aceleración del cuerpo, cuyo origen está en realidad, en el hecho de que el sistema de observación está rotando.
Un ejemplo canónico de efecto Coriolis es el experimento imaginario en el que disparamos un obús desde el Ecuador en dirección norte. El cañón está girando con la tierra hacia el este y, por tanto, imprime al obús esa velocidad (además de la velocidad hacia adelante de la carga de impulsión). Al viajar el obús hacia el norte, sobrevuela puntos de la tierra cuya velocidad lineal hacia el este va disminuyendo con la latitud creciente. La inercia del obús hacia el este hace que su velocidad angular aumente y que, por tanto, adelante a los puntos que sobrevuela. Si el vuelo es suficientemente largo (ver cálculos al final del artículo), el obús caerá en un meridiano situado al este de aquél desde el cual se disparó, a pesar de que la dirección del disparo fue exactamente hacia el norte. Análogamente, una masa de aire que se desplace hacia el este sobre el ecuador aumentará su velocidad de giro con respecto al suelo en caso de que su latitud disminuya. Finalmente, el efecto Coriolis, al actuar sobre masas de aire (o agua) en latitudes intermedias, induce un giro al desviar hacia el este o hacia el oeste las partes de esa masa que ganen o pierdan latitud de forma parecida a como gira la bolita del ejemplo.
Introducción
La tendencia del giro varía según el hemisferio considerado
La fuerza de Coriolis es una fuerza ficticia que aparece cuando un cuerpo está en movimiento con respecto a un sistema en rotación y se describe su movimiento en ese referencial. La fuerza de Coriolis es diferente de la fuerza centrífuga. La fuerza de Coriolis siempre es perpendicular a la dirección del eje de rotación del sistema y a la dirección del movimiento del cuerpo vista desde el sistema en rotación. La fuerza de Coriolis tiene dos componentes:
• una componente tangencial, debido a la componente radial del movimiento del cuerpo, y
• una componente radial, debido a la componente tangencial del movimiento del cuerpo.
La componente del movimiento del cuerpo paralela al eje de rotación no engendra fuerza de Coriolis.
El valor de la fuerza de Coriolis es:
donde:
• es la masa del cuerpo.
• es la velocidad del cuerpo en el sistema en rotación .
• es la velocidad angular del sistema en rotación vista desde un sistema inercial.
• indica producto vectorial.
Historia
En 1835, Gaspard-Gustave de Coriolis, en su artículo Sur les équations du mouvement relatif des systèmes de corps, describió matemáticamente la fuerza que terminó llevando su nombre. En ese artículo, la fuerza de Coriolis aparece como una componente suplementaria a la fuerza centrífuga experimentada por un cuerpo en movimiento relativo a un referencial en rotación, como puede producirse, por ejemplo, en los engranajes de una máquina. El razonamiento de Coriolis se basaba sobre un análisis del trabajo y de la energía potencial y cinética en los sistemas en rotación. Ahora, la demostración más utilizada para enseñar la fuerza de Coriolis utiliza los útiles de la cinemática.
Esta fuerza comenzó a aparecer en la literatura meteorológica y oceanográfica sólo hasta finales del siglo XIX. El término fuerza de Coriolis apareció a principios del siglo XX.
Formulación y demostración
Para demostrar la expresión analítica expresada en la introducción, existen dos aproximaciones diferentes: por conservación del momento angular o por derivación en base móvil. A continuación se explican ambas.
Demostración por conservación del momento angular
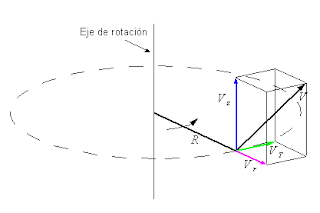
En un sistema de coordenadas cilíndricas, la velocidad (en negro) de un punto puede descomponerse en una velocidad radial (en magenta), una velocidad axial (en azul) y una velocidad tangencial (en verde).
Recordemos que cuando un observador en un sistema no inercial, como lo es un sistema en rotación, trata de comprender el comportamiento de su sistema como si fuese un sistema inercial, ve aparecer fuerzas ficticias. En el caso de un sistema en rotación, el observador ve que todos los objetos que no están sujetos se alejan de manera radial como si actuase sobre ellos una fuerza proporcional a sus masas y a la distancia a una cierta recta (el eje de rotacion). Esa fuerza es la fuerza centrífuga que hay que compensar con la fuerza centrípeta para sujetar los objetos. Por supuesto, para un observador externo, situado en un sistema inercial (sistema fijo), la única fuerza que existe es la fuerza centrípeta, cuando los objetos están sujetos. Si no lo están, los objetos tomarán la tangente y se alejarán del eje de rotación.
Si los objetos no están inmóviles con respecto al observador del sistema en rotación, otra fuerza ficticia aparece: la fuerza de Coriolis. Visto del sistema en rotación, el movimiento de un objeto se puede descomponer en una componente paralela al eje de rotación, otra componente radial (situada sobre una línea que pasa por el eje de rotación y perpendicular a éste), y una tercera componente tangencial (tangente a un círculo centrado en el eje y perpendicular a éste) (ver dibujo).
Un objeto que se desplaza paralelamente al eje de rotación, visto de un sistema fijo, gira con el sistema en rotación a la misma velocidad angular y radio constante. La única fuerza que actúa sobre el objeto es la fuerza centrípeta. El observador del sistema en rotación sólo ve la fuerza centrífuga contra la cual hay que oponerse para que se quede a la misma distancia del eje.
Cuando se reduce el radio de rotación de un cuerpo sin aplicar un torque, el momento angular se conserva y la velocidad tangencial aumenta. En cambio, si se obliga el cuerpo a conservar la misma velocidad angular, la velocidad tangencial disminuye. El dibujo está visto desde un sistema fijo (inercial).
Supongamos que un observador en el sistema en rotación mantiene una masa a una distancia del eje de rotación mediante un hilo de masa despreciable. El observador tira del hilo y modifica ligeramente el radio de rotación de la masa de . Eso le ha tomado un tiempo . Como el momento dinámico es nulo, el momento angular de la masa se conserva. Si llamamos la velocidad de la masa, la conservación del momento angular nos dice:


El signo menos indica que cuando el radio aumenta la velocidad tangencial disminuye.
Si la masa se moviese siguiendo una trayectoria radial, fija con respecto al sistema en rotación, conservando en consecuencia la misma velocidad angular del sistema en rotación, su velocidad lineal habría aumentado de (o disminuido, si es negativo). Para un observador fijo, entre la velocidad de la masa que se ve obligada a seguir una trayectoria radial y la velocidad de la masa que conserva su momento angular hay una diferencia de:
Como el objeto no está sujeto al sistema en rotación, el observador en ese sistema ve la masa tomar una velocidad lateral . Eso lo interpreta como la aplicación de una fuerza lateral (de Coriolis). Si el cambio de velocidad tomó segundos, la aceleración de Coriolis será (en valor absoluto):
,
donde es la velocidad radial. Esa aceleración corresponde a una fuerza (de Coriolis) de:
Ocupémonos de un objeto con velocidad tangencial vista por el observador en el sistema en rotación. Esta vez, la misma masa tenida por un hilo tiene una velocidad angular diferente del sistema en rotación. Para el observador en el sistema en rotación, las fuerzas que ve aplicadas a la masa para que siga una trayectoria circular son: la fuerza centrífuga que ve aplicada en todos los objetos, más la fuerza centrífuga debido a la rotación aparente de la masa . Pero eso no basta. Hay aún otra fuerza aparente, y es precisamente la fuerza de Coriolis. Calculemos la fuerza centrípeta que ve un observador fijo. La velocidad tangencial que ve es . Para este observador, la fuerza centrípeta que mantiene la masa a distancia constante es:
El primer término es la fuerza centrífuga común a todos los objetos que giran con el sistema en rotación. El tercero es la fuerza centrífuga debida a la rotación de la masa con respecto al sistema en rotación. Y el segundo término es la fuerza de Coriolis. Es un término suplementario debido al hecho de que la fuerza centrífuga depende del cuadrado de la velocidad tangencial y no puede obtenerse sumando las fuerzas centrífugas debido a velocidades parciales. La fuerza de Coriolis es:
Como hemos dicho, esa fuerza es radial.
Meteorología, oceanografía y fuerza de Coriolis
El ejemplo más nombrado de manifestación del efecto Coriolis se da cuando masas de aire o de agua se desplazan siguiendo meridianos terrestres, y su trayectoria y velocidad se ven modificadas por él. En efecto, los vientos o corrientes oceánicas que se desplazan siguiendo un meridiano se desvían acelerando en la dirección de giro (este) si van hacia los polos o al contrario (oeste) si van hacia el ecuador. La manifestación de estas desviaciones produce, de manera análoga al giro de la bolita mostrado al principio, que las borrascas giren en el hemisferio sur en el sentido de las agujas del reloj y, en el hemisferio norte, en sentido contrario.
El efecto de la fuerza de Coriolis deberá considerarse siempre que se estudie el movimiento de fluidos y también el de cualquier objeto móvil sobre esferas o superficies planas en rotación. Esto incluye a los planetas gaseosos del sistema solar, el Sol y todas las estrellas y, en el planeta Tierra, el movimiento de las aguas de los ríos, los lagos, los océanos y, por supuesto, de la atmósfera. El efecto de Coriolis predice que siempre que se observen los movimientos giratorios de esos cuerpos, los vórtices seguirán la norma descrita para las borrascas y anticiclones terrestres.
Además de su influencia sobre la atmósfera, es muy notoria la que tiene también sobre la circulación oceánica. En las cuencas que tienen la forma apropiada (como, por ejemplo, la cuenca del Atlántico norte y la del Atlántico sur), el efecto Coriolis desvía a las corrientes marinas hacia la derecha en el hemisferio norte y hacia la izquierda en el hemisferio sur, de la misma manera que sucede con la circulación general de los vientos.
Las excepciones o modificaciones de este patrón general de la circulación general de los océanos tienen que ver con la disposición de las costas y la compensación introducida por las corrientes cálidas que van, en los océanos, de las costas orientales de la zona intertropical hacia las occidentales de las zonas templadas de los continentes (Corriente del Golfo y de Kuro Shivo, especialmente). Además, en los océanos, lo mismo que sucede en la atmósfera, se produce una especie de convergencia en las latitudes ecuatoriales por la fuerza centrífuga del movimiento de rotación: tanto el océano como la atmósfera tienen un abombamiento ecuatorial por la rotación terrestre, de varios metros de altura en el caso de los océanos y de varios kilómetros en la atmósfera. A su vez, este "abombamiento" ocasiona una especie de obstáculo a la libre circulación y al libre intercambio de energía (oceánica y atmosférica) entre los dos hemisferios. La circulación en la zona ecuatorial es, por lo tanto, de este a oeste, tanto en lo que respecta a las corrientes ecuatoriales del norte y del sur como con respecto a los alisios del noreste en el hemisferio norte y del sureste en el hemisferio sur. Por último, lo que hemos denominado abombamiento ecuatorial de los océanos tiene varias consecuencias: entre ellas, la formación de lo que se ha denominado contracorrientes ecuatoriales también del norte y del sur, definidas e identificadas en muchos atlas y libros de geografía y de ciencias de la Tierra, y la desviación hacia las zonas subtropicales y templadas: de nuevo, hacia la derecha en el hemisferio norte y hacia la izquierda en el hemisferio sur.
Efectos de la fuerza de Coriolis
Una de las raras ocasiones en la cual una persona puede sentir la fuerza de Coriolis es cuando trata de caminar siguiendo una trayectoria radial en un tiovivo (o carrusel). Cuando la persona se aleja del eje de rotación, sentirá una fuerza que la empuja en el sentido contrario a la rotación: es la fuerza de Coriolis.
Cuando una persona se aleja o se acerca del eje de rotación a una velocidad de 1 m/s en un tiovivo que gira a 10 vueltas por minuto, la aceleración de Coriolis es:
Se trata, por consiguiente, de una aceleración lateral 46 veces más pequeña que el peso de la persona. Para una persona de 70 kg, eso corresponde a una fuerza lateral igual al peso de 1,5 kg. No es mucho pero, poniendo atención, puede sentirse.
Objetos que se desplazan sobre la Tierra
La Tierra gira mucho más lentamente que un tiovivo. Su velocidad angular es de radianes por día sideral (23 h, 56 m, 4,1 s) es decir . La aceleración de Coriolis debido a la rotación de la Tierra es mucho menor.
Cuando un cuerpo sigue una trayectoria norte-sur sobre la Tierra (siguiendo un meridiano), la componente radial de su velocidad (la velocidad a la cual el cuerpo se acerca o se aleja del eje de rotación terrestre) depende de la latitud del cuerpo. Es fácil ver que la componente radial es . Cuando el cuerpo está cerca del ecuador, su distancia respecto al eje de la Tierra no cambia. Si la trayectoria del cuerpo es este-oeste y sigue un paralelo, su distancia respecto al eje terrestre no varía, pero ya hemos visto que sentirá una aceleración de Coriolis dirigida hacia el eje de la Tierra que vale . La componente paralela a la superficie de la Tierra depende de la latitud y es: .
Vemos que en los dos casos, visto desde la Tierra, un cuerpo que se desplaza sobre la superficie de la Tierra siente una aceleración lateral de valor dirigida hacia la derecha de la velocidad.
Un cuerpo que se desplaza con una velocidad de 1 m/s, sin interacción con el suelo, a una latitud de 45° encuentra una aceleración lateral de Coriolis igual a:
,
lo cual corresponde a una fuerza lateral aproximadamente 100 000 veces menor que el peso del cuerpo. Dicho de otra manera, la trayectoria se desvía hacia la derecha como si el terreno estuviese inclinado hacia la derecha de 1 milímetro cada 100 metros.
Si se trata de un avión cuya velocidad es 900 km/h (250 m/s), la aceleración será 250 veces mayor. El efecto será darle al avión una trayectoria circular de 4,850 km de diámetro (a una latitud de 45°):
Por supuesto, el piloto corregirá esta desviación, pero no parece posible que pueda distinguirla de los efectos del viento o de los errores de reglaje de la posición neutra de los alerones de dirección y de profundidad.
Balística
Tomemos el caso de un obús, situado a una latitud de 45° y que tira un proyectil a 110 km de distancia. El ángulo de tiro para esa distancia es de 45°. Si se desprecia el efecto de los rozamientos con el aire, la velocidad horizontal del proyectil es de 734 m/s, y el tiempo de vuelo es de 150 segundos. La aceleración de Coriolis será:
La distancia lateral creada por la aceleración de Coriolis es:
Esa distancia corresponde a un error en el ángulo de tiro de 0,44°. Las opiniones divergen sobre la importancia de este error, comparado con la influencia de otras fuerzas y, sobre todo, con la fuerza provocada por el efecto Magnus sobre proyectiles que giran axialmente.
Para cañones de menor alcance, el error en el ángulo de tiro es aún menor. Por ejemplo, para un proyectil cuyo alcance es de 20 km y cuya velocidad media es la misma, el error del ángulo es 25 veces menor.
Aplicación práctica
Una aplicación práctica de la fuerza de Coriolis es el caudalímetro másico, un instrumento que mide el caudal másico de un fluido que circula a través de una tubería. Este instrumento fue comercializado en 1977 por Micro Motion Inc.
Los caudalímetros normales miden el caudal volumétrico, el cual es proporcional al caudal másico sólo cuando la densidad del fluido es constante. Si el fluido tiene una variación de densidad o contiene burbujas, entonces el caudal volumétrico, multiplicado por la densidad, no será exactamente igual al caudal másico. El caudalímetro másico de Coriolis funciona aplicando una fuerza de vibración a un tubo curvado a través del cual pasa el fluido. El efecto Coriolis crea una fuerza en el tubo perpendicular a ambas direcciones: la de vibración y la dirección de la corriente. Esta fuerza se mide para obtener el caudal másico. Los caudalímetros de Coriolis pueden usarse además con fluidos no newtonianos, en los cuales los caudalímetros normales tienden a dar resultados erróneos. El mismo instrumento puede usarse para medir la densidad del fluido. Este instrumento tiene una novedad adicional, que consiste en que el fluido está en un tubo liso, sin partes móviles, que no necesita